Introduction :
La propagation dans un câble coaxial est régie pas les phénomènes physiques relatifs à la propagation d'ondes : somme d'une onde incidente et onde rétrograde. La superposition de ces deux ondes forme une onde qui dépend du temps t mais également de abscisse x. Ces effets sont visibles dès que la longueur d'onde est inférieur à la longueur du câble. On mesure les effets de cette onde par l'intermédiaire de la tension V(x,t) et/ou du courant I(x,t). Trois grands paramètres sont généralement caractérises sur un câble coaxial :
Atténuation (en m^-1 ou en dB/100m) :
En régime continu : uniquement dépendante des éléments résistifs du montage (résistance du câble et partie résistive de la charge)
En régime harmonique : dépendant principalement de l'effet de peau.
Coefficient de réflexion qui impose le rapport entre amplitude de la tension réfléchie et la tension incidente (indépendant de l'abscisse) et dont la phase dépend de l'abscisse.
Rapport d'ondes stationnaires (ROS) : caractérise en régime harmonique le taux de désadaptation d'un câble coaxial fermé sur une charge d'impédance Zload.
Matériel à disposition
Afin de mener à bien ce TP, nous avons besoin de plusieurs instruments, parmi les instruments disponibles, nous utiliserons un générateur de fonction Agilent 33220A, un oscilloscope Keysight DSOX1204G, deux câbles coaxiaux de 50cm et 100m d'impédance carractéristique Z0 = 50Ω, trois Té BNC, une charge BNC de 50Ω, un court-circuit BNC, un potentiomètre ainsi qu'un multimètre en mode ohmètre comme le montre la figure 1 ci-dessous.

GBF Agilent 33220A
oscilloscope Keysight DSOX1204G

Té BNC

câble coaxial 50Ω

multimètre générique

potentiomètre
figure 1 : Matériel utilisé
Mesure de l'atténuation dans un câble coaxial
La première partie de ce TP consiste en la mesure de l'atténuation du câble coaxial. Comme nous l'avons indiqué, les pertes dépendent de la fréquence. En régime continu ou aux très basses fréquences, la résistance linéique r (en Ω/m) s'écrit simplement r = p/S ou S est la section réelle du conducteur. Aux hautes fréquences, il faut tenir compte de l'effet de peau et la résistance linéique r augmente avec la fréquence. La densité du courant n'est plus homogène dans le conducteur, le courant circule uniquement à la périphérie, la section utile au passage du courant devient inférieure à S.
Mesures préliminaires
Tout d'abord, nous connectons le générateur de fonction à l'oscilloscope via un câble d'une longueur de 50cm et d'impédance caractéristique Zc de 50Ω comme le montre la figure 2 ci-dessous.

figure 2 : branchement effectué pour les mesures préliminaires
Ensuite, nous réglons le générateur de fonction pour visualiser sur l'oscilloscope un signal sinusoïdal d'amplitude 6 Vcc et de fréquence f = 1 kHz. Comme le montre la figure 2 ci-dessous nous avons donc réglé le générateur à f = 1kHz et Vcc = 4,92V.

Ensuite, nous réglons le générateur de fonction pour visualiser sur l'oscilloscope un signal sinusoïdal d'amplitude 6 Vcc et de fréquence f = 1 kHz. Comme le montre la figure 2 ci-dessous nous avons donc réglé le générateur à f = 1kHz et Vcc = 2,8V.
Nous pouvons donc observer un signal sinusoidal d'amplitude 6 Vcc et de fréquance 1kHz à l'écran de l'oscilloscope comme le montre la figure ci-contre
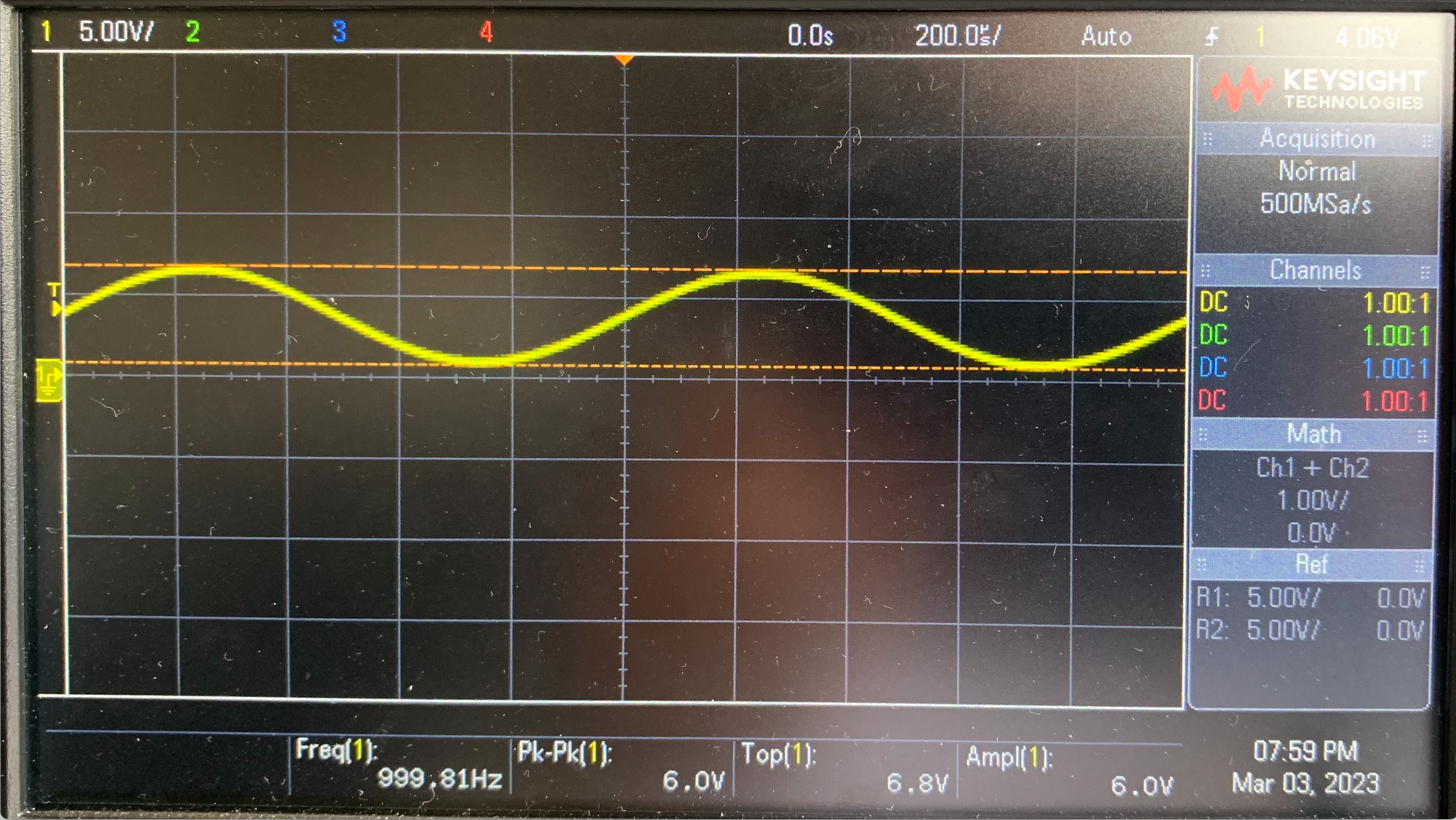
Nous placons ensuite en Té BNC à l'entrée de la voie 1 de l'oscilloscope afin d'y brancher un bouchon BNC de 50Ω, nous obtenons ainsi le signal représenté en figure 3 ci-dessous.

figure 3 : signal observé à l'écran de l'oscilloscope
Mesure de l'attenuation aux très basses fréquences
Nous connectons le générateur de finctoin à l'oscilloscope via un cable d'impédance caractéristique Zc = 50Ω et de longueur d'environ 50cm. On utilisera la sortie 50Ω du générateur. Puis, nous connectons par l'intermédiaire d'un Té BNC, l'entrée du câble de 100m de longueur à la voie 1 de l'oscilloscope. Sur la voie 2, le point milieu du câble et sur la voie 3, l'extrémité du câble et le bouchon 50Ω avec un Té BNC comme le montre la figure 4 ci-dessous.
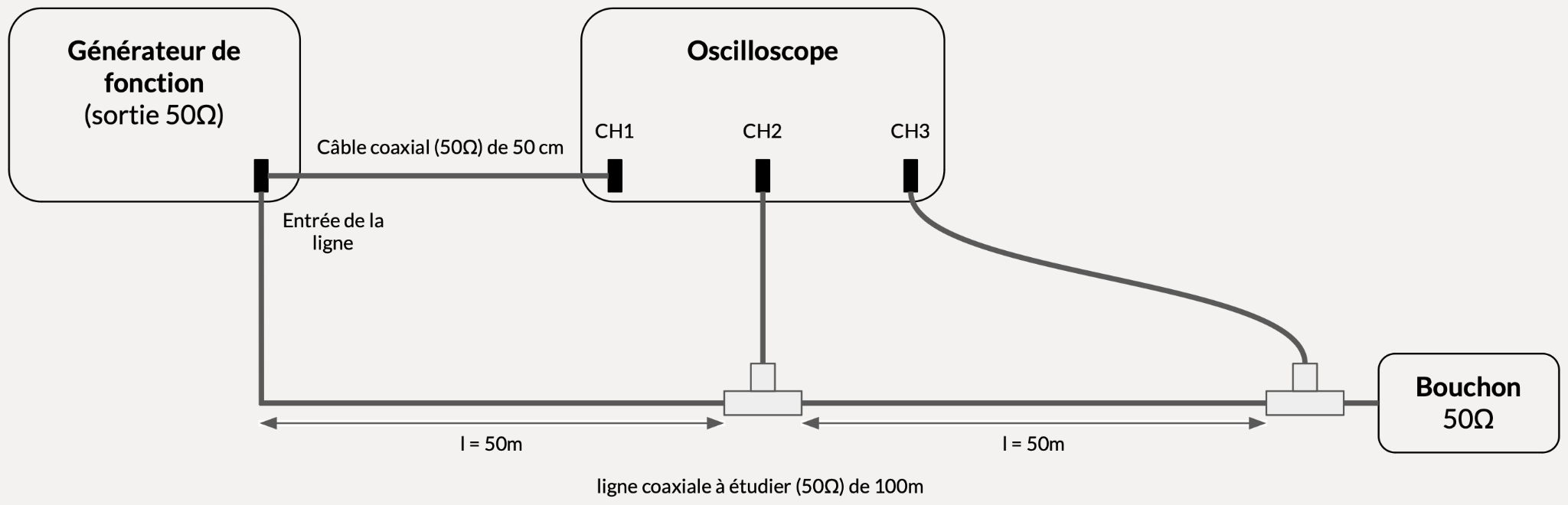
figure 4 : Branchement effectué pour la mesure de l'atténuation à très basse fréquence
Ensuite, nous réglons le GBF afin de visualiser à l'oscilloscope une signal sinusoidal d'amplitude 6 Vpp, nous avons donc Vgbf = 4,92V comme le montre la figure 5 ci-dessous

réglage du GBF
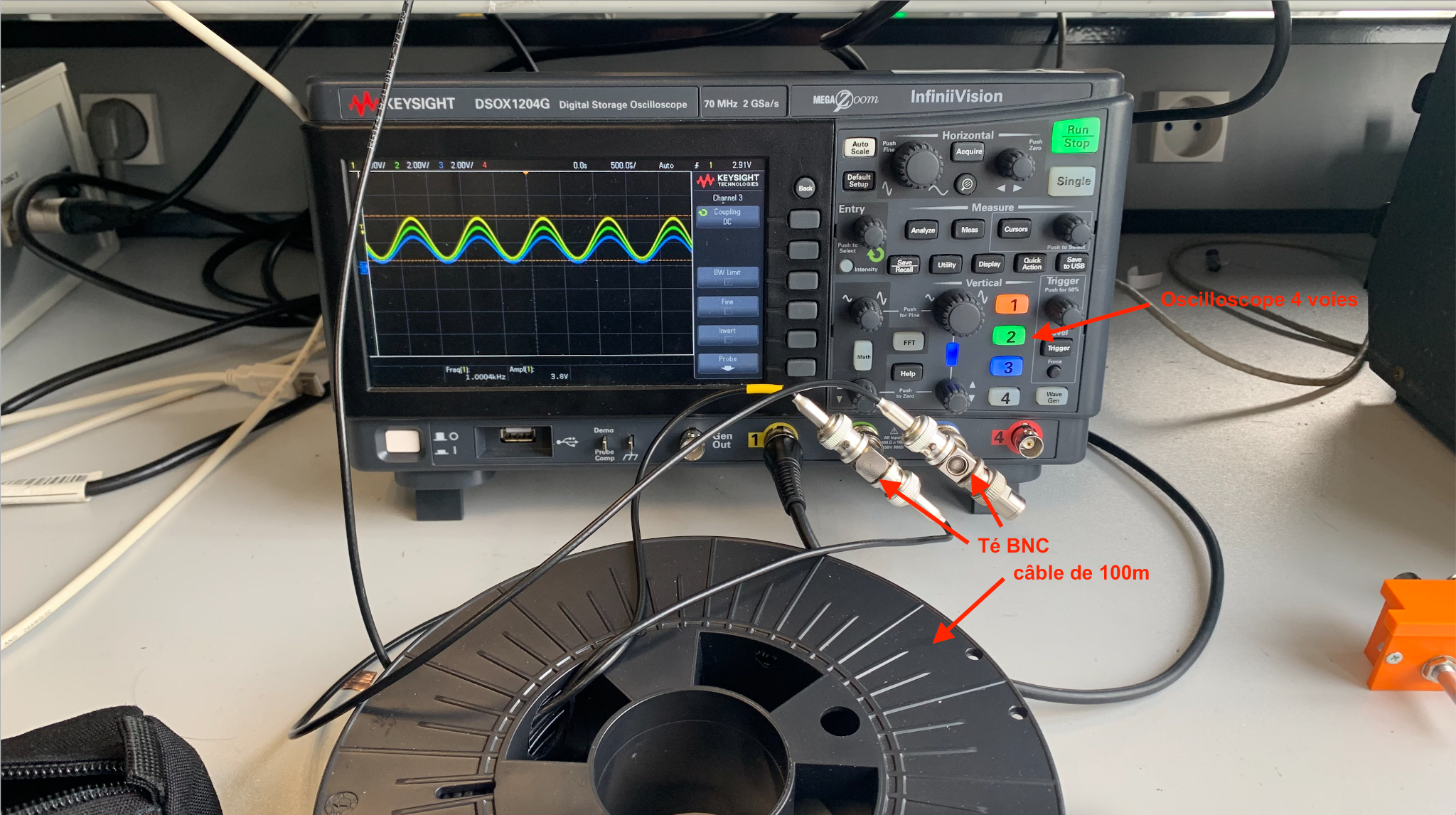
câblage du montage de la figure 3
figure 5 : Réglage du GBF et câblage du montage de la figure 3
Nous pouvons donc observer le résultat ci-contre à l'écran de l'oscilloscope, nous relevons une amplitude de 6,05 Vpp sur CH1 (en jaune), 4,96 Vpp sur CH2 (en vert) et 3,86 Vpp sur CH3 (en bleu)
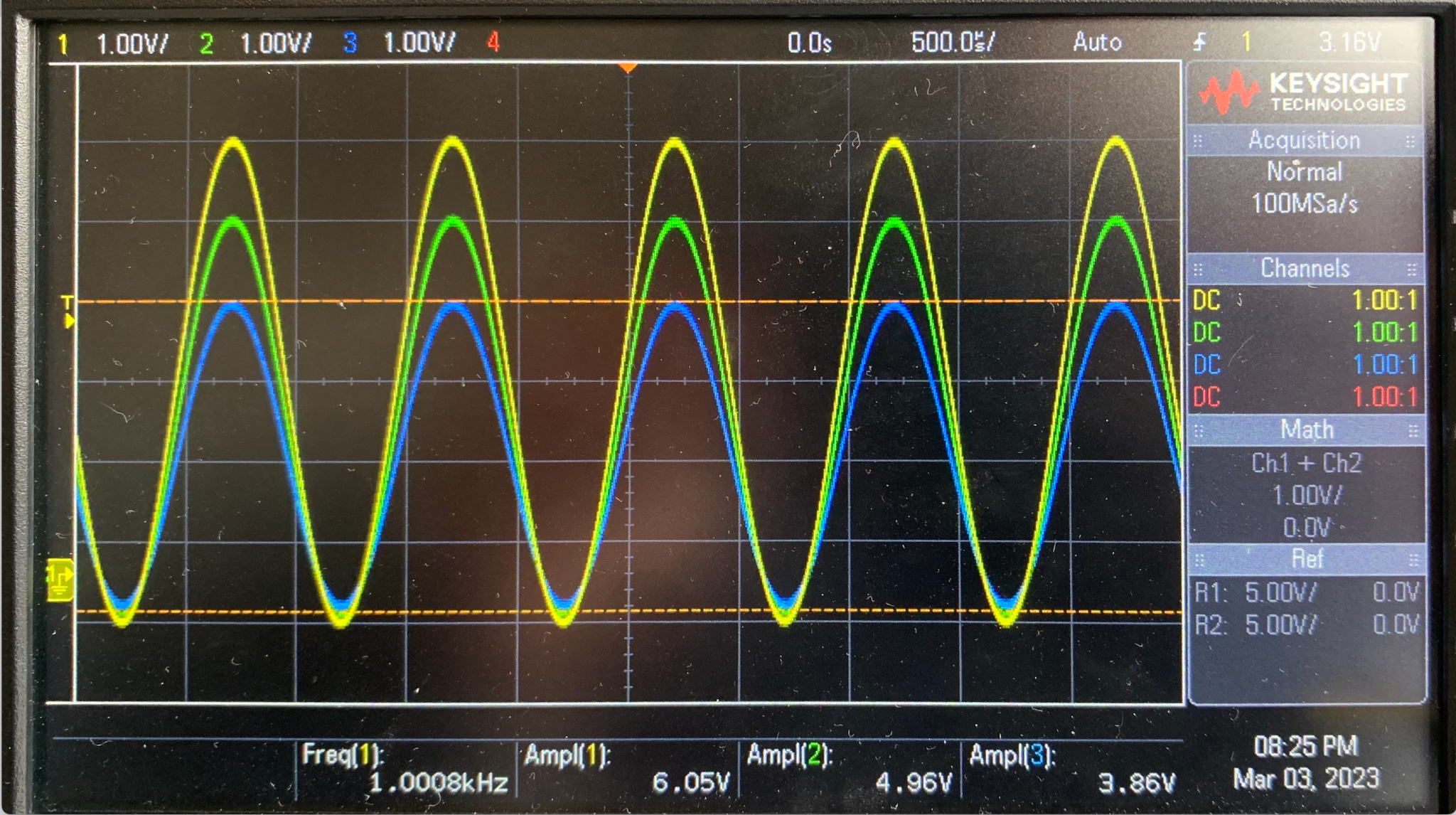
Nous pouvons donc calculer l'atténuation dans le câble en dB : 20log(Vmax/Vmin) = 20log(6,05/3,86) = 3,90 dB à f = 1 kHz.
Mesure de l'attenuation en fonction de la fréquence
Nous souhaitons analyser l'atténuation du câble coaxial en fonction de la fréquence. On conserve les brenchements réalisés pour les manipulation sprécédentes mais on fait varier le fréquence du signal de 1 kHz à 20Mhz.
Nous obtenons ainsi 12 mesures dont on peut retrouver 6 d'entre elles en figure 6 ci-dessous.
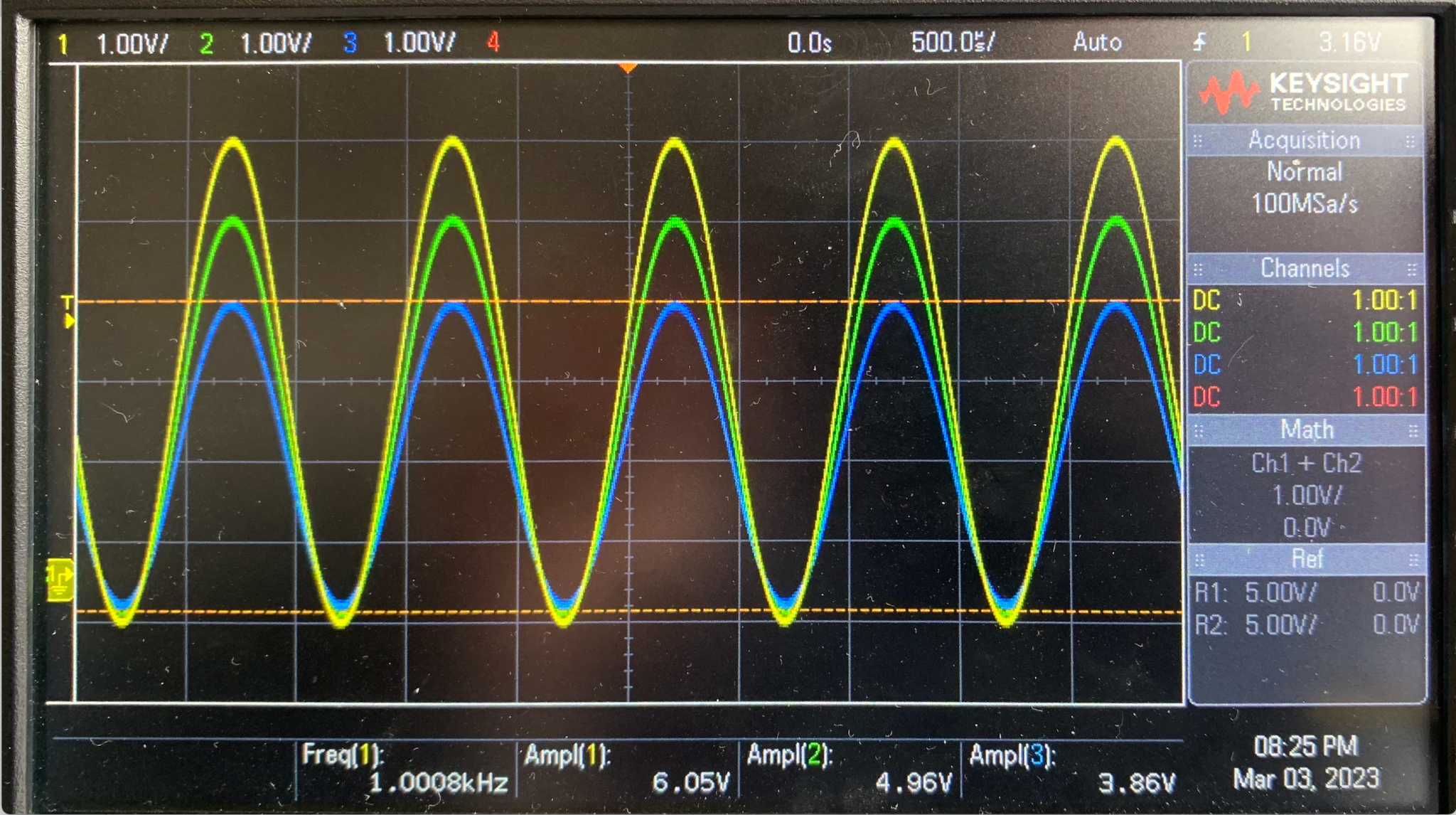
f = 1kHz
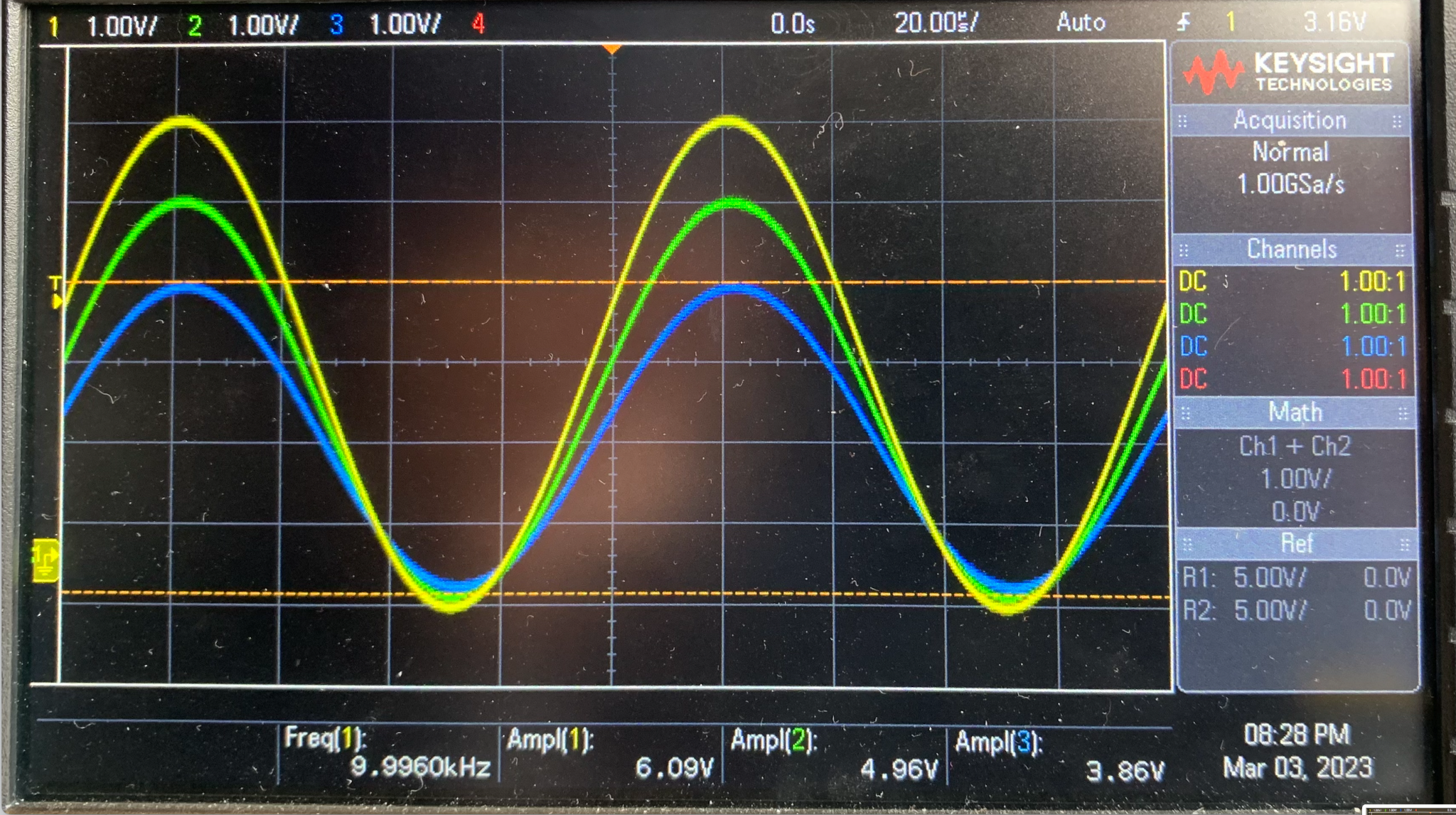
f = 10kHz
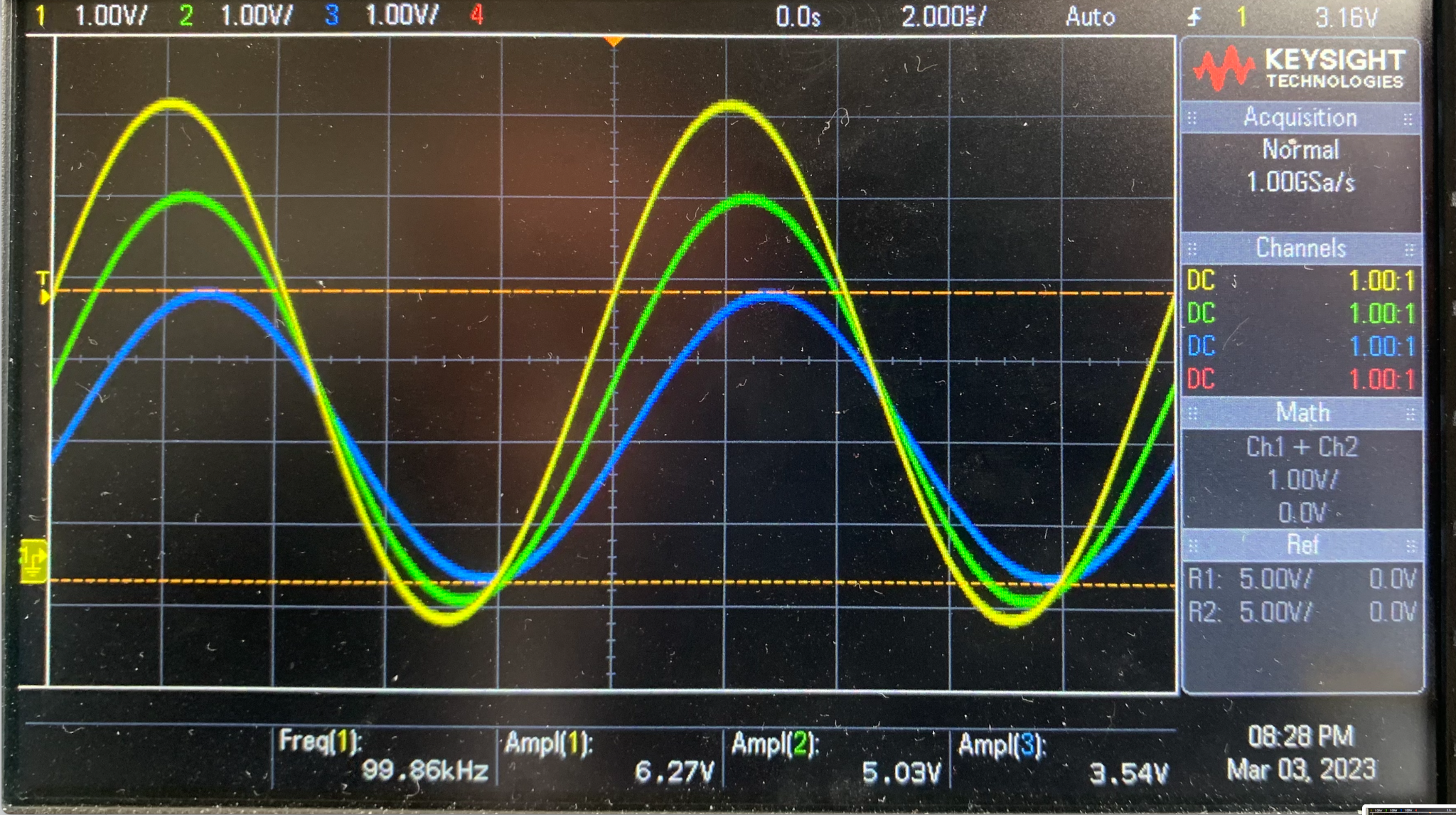
f = 100kHz
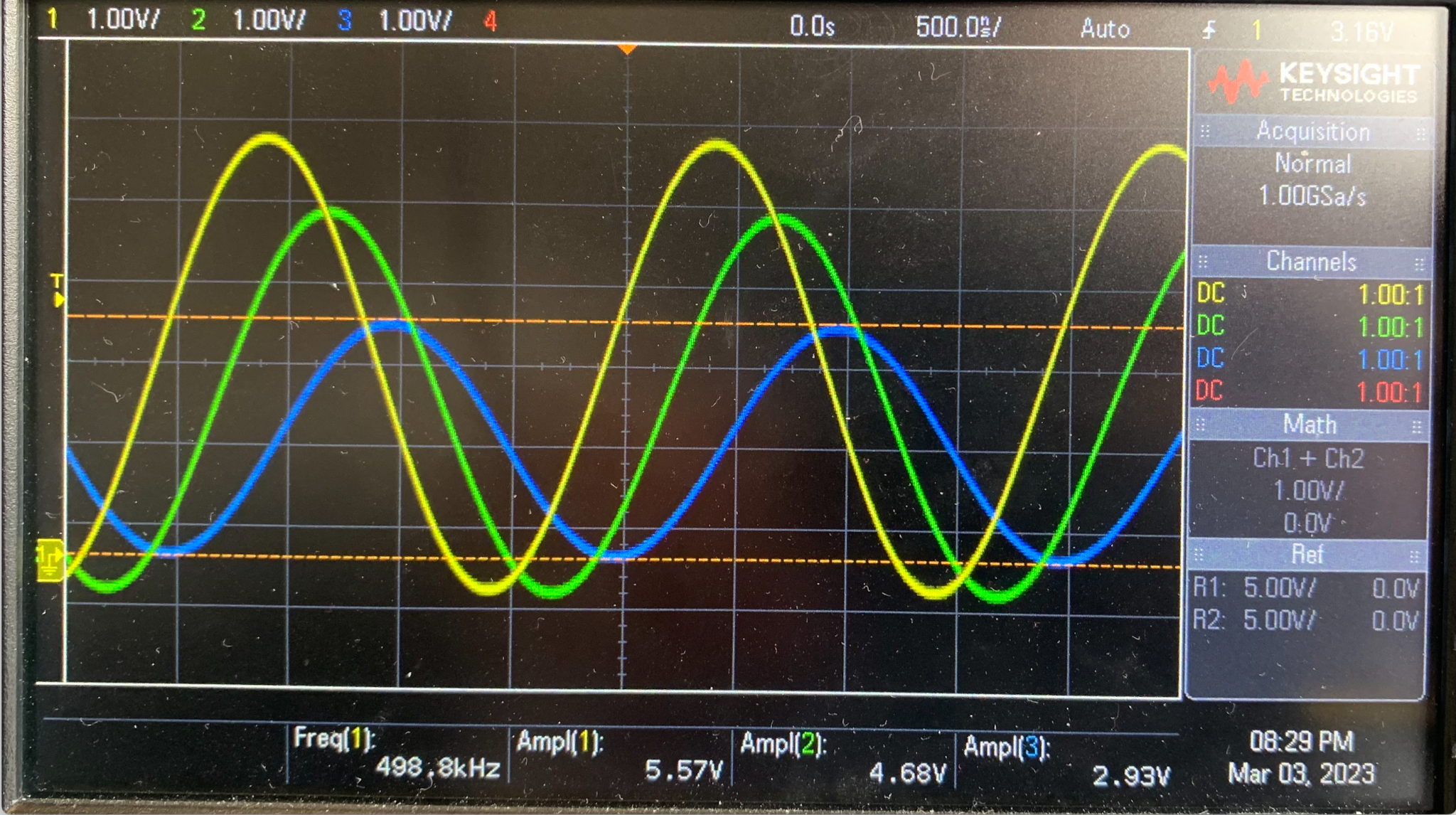
f = 500kHz
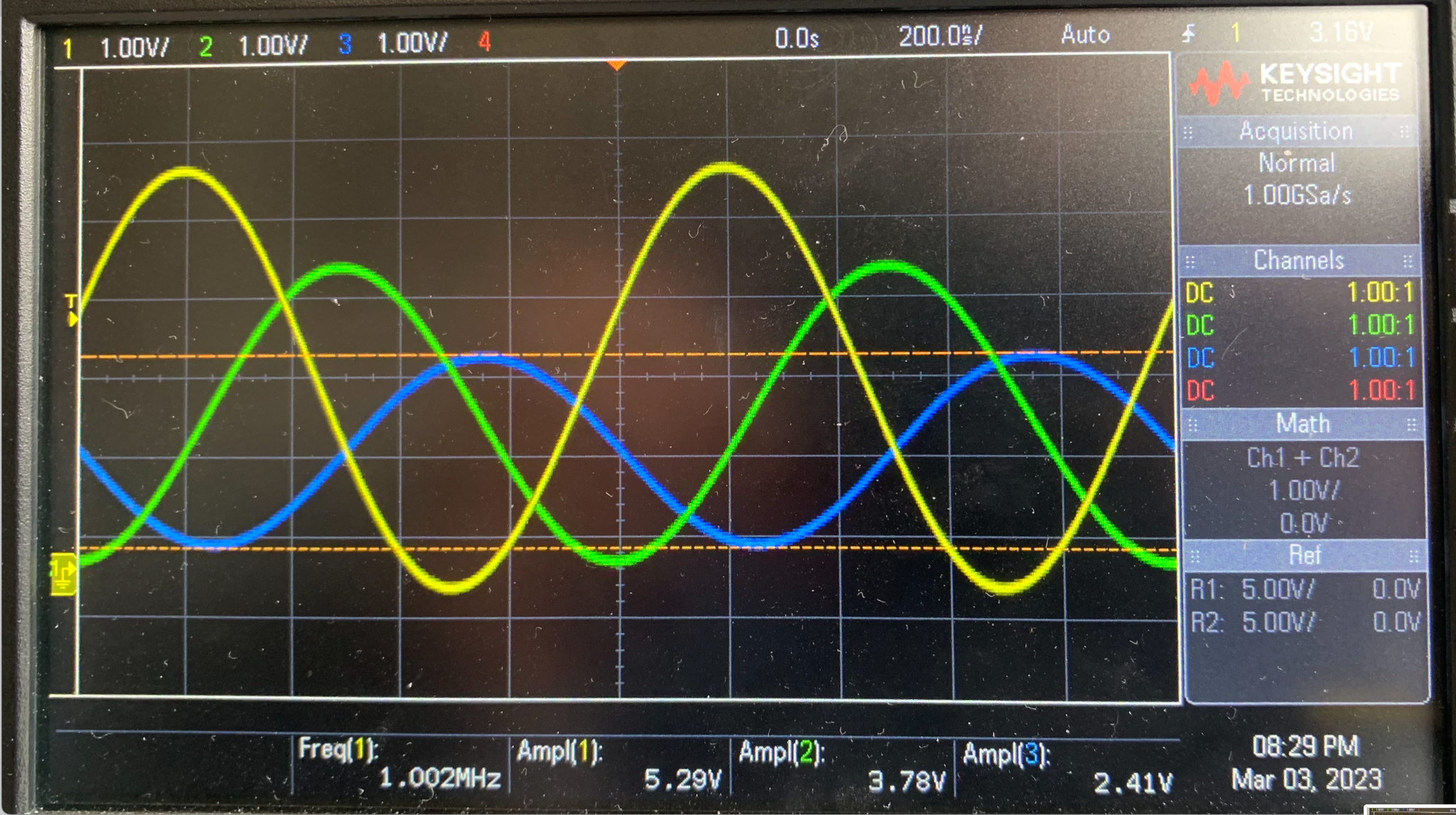
f = 1GHz
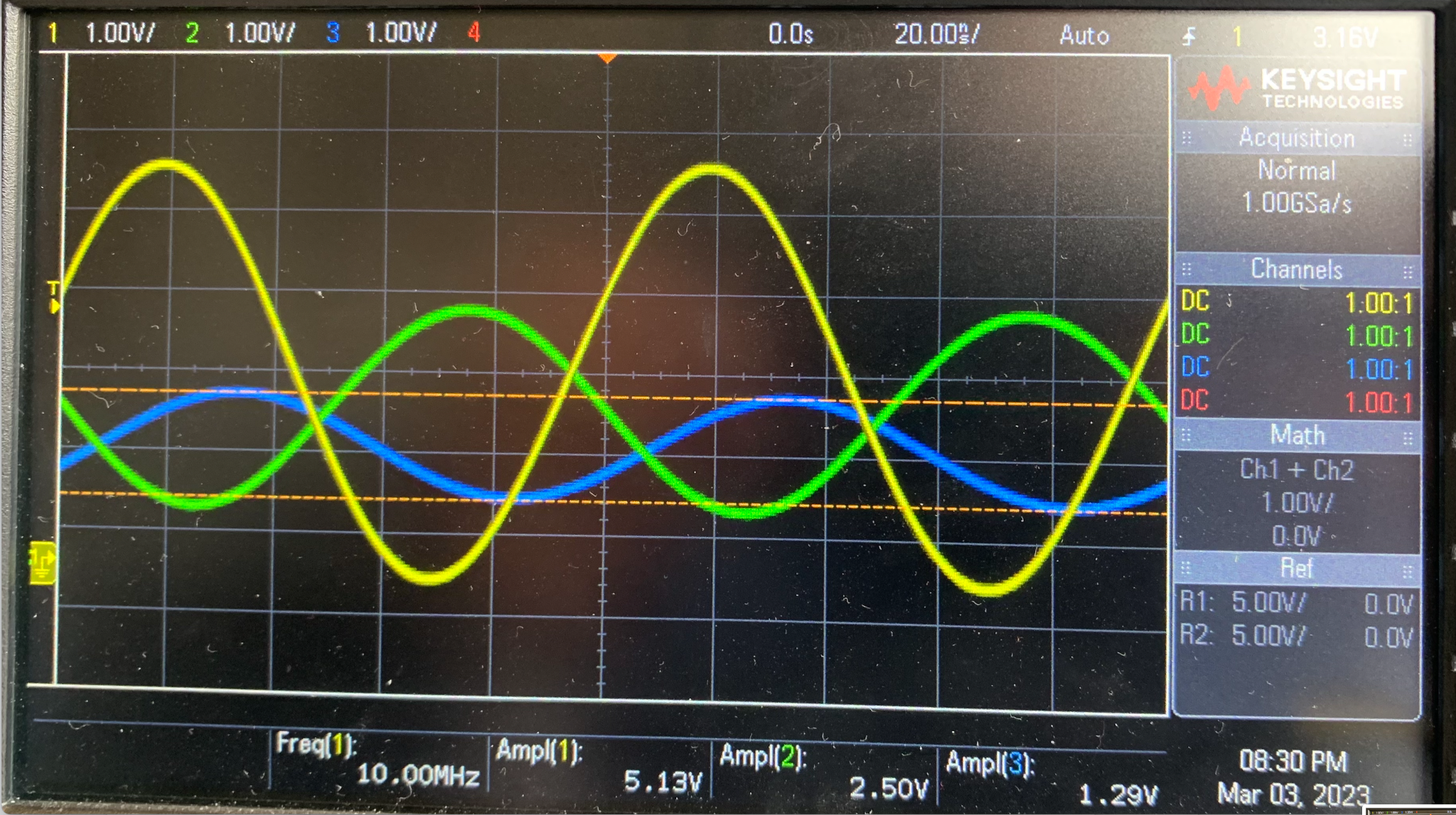
f = 10GHz
figure 6 : mesure de l'amplitude pour différentes fréquences
A l'aide des es mesures nous pouvons donc dresser le tableau ci-contre qui présente l'amplitude mesurée à l'entrée et à la sortie du câble (V1 et V3) en fonction de la fréquence ainsi que l'attenutaion en dB.

A l'aide du tableau ci-dessus, nous pouvons donc tracer le graphique représentant l'attenuation en dB en fonction de la fréquence en figure 7 ci-dessous

figure 7 : tracé de l'attenuation en fonction de la fréquence
Propagation en régime impulsionnel
Détermination des constantes linéiques d'un câble coaxial
Tout d'abord, nous réalisons le câblage représenté dans la figure 8 ci-dessous

figure 8 : schéma de câblage réalisé
Nous réglons ensuite le GBF afin de générer un signal d'impultions périodiques positives d'ammplitude A = 4V, de durée θ = 400ns et de fréquence f = 100kHz, afin de vérifier nos réglages, nous vérifions le signal de sortie à l'aide de l'oscolloscope comme le montre la figure 9 ci-dessous.
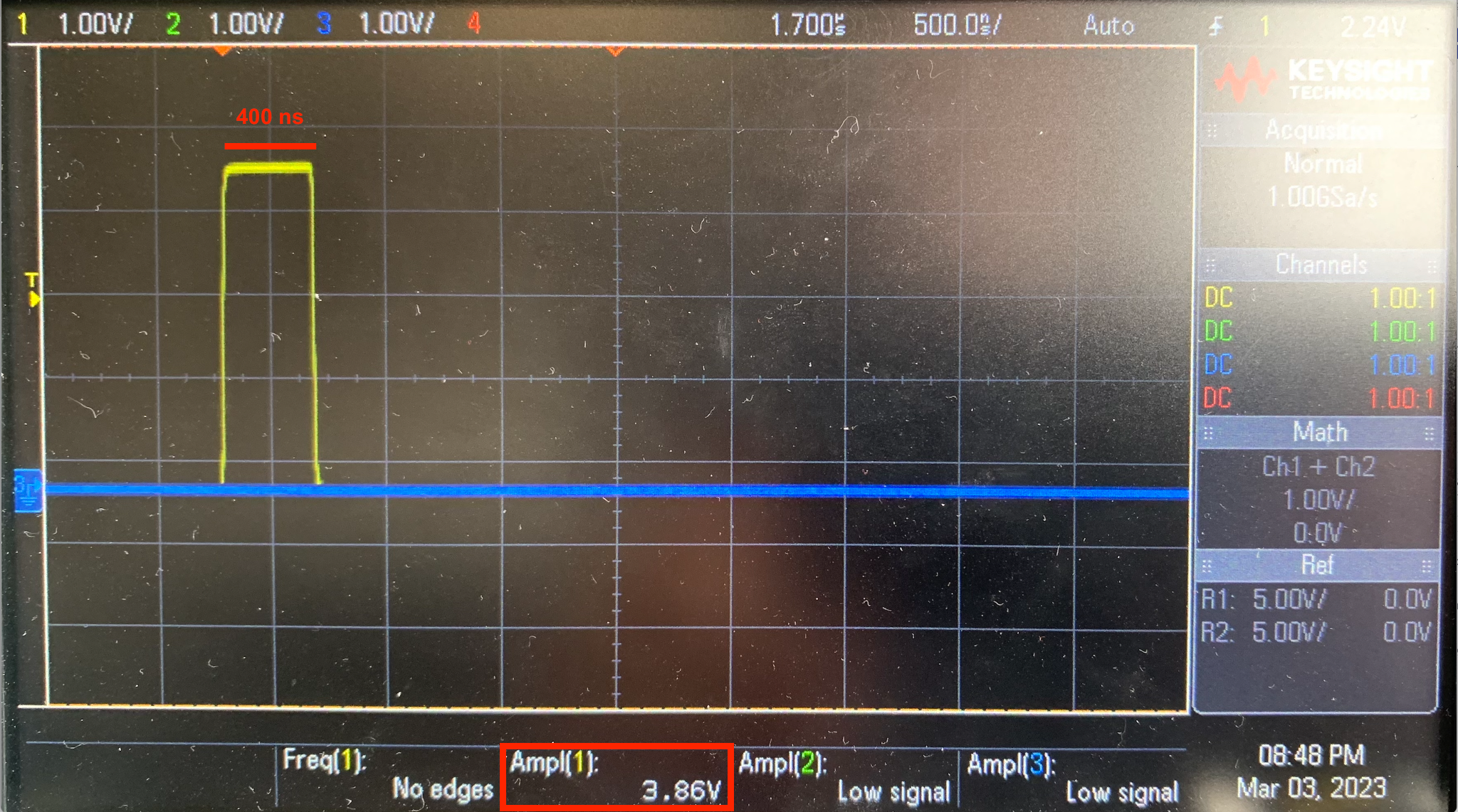
figure 9 : vérification du signal envoyé par le GBF
Nous pouvons donc conclure que le signal envoyé par le GBF est correct, nous reconnectons ensuite l'entrée de la ligne sur l'entrée du GBF. Nous pouvons donc déterminer la durée de propagation τ d'une impultion d'un bout à l'autre du câble afin d'en déduire la vitesse de propagation dans le câble, pour cela nous relevons l'écran de l'oscilloscope comme le montre la figure 10 ci-dessous.
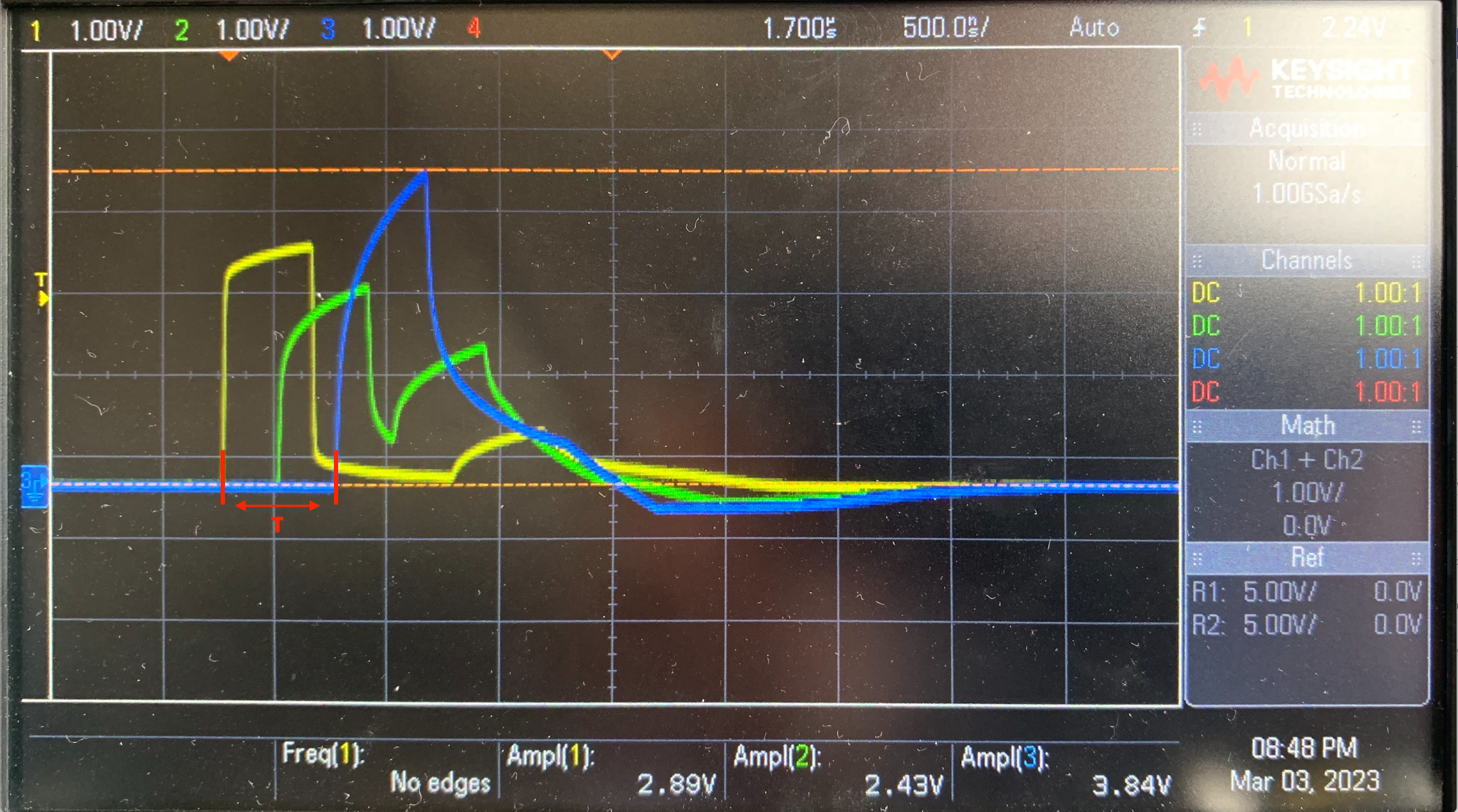
figure 10 : mesure du temps de propagation
Nous mesurons donc, τ = 250ns et donc v = d/τ = 50/250e-9 = 2e8 m/s
Nous chargons ensuite l'extrémité du câble par une résistance variable (0-100Ω). Nous pouvons ensuite régler la valeure de la résistance jusqu'à atteindre la disparition des impultions réfléchies pour ensuite mesurer sa valeure à l'ohmètre pour en déduire la valeure de l'impédance carractéristique Zc du câble.

Nous avons donc le schéma de câblage ci-contre
Nous actionnons donc la résistance variable jusqu'à obtenir le résultat à l'oscilloscope ci-contre
Dans la figure ci-contre nous pouvons donc voir qu'auccun signal n'est réfléchi vers la source, nous somme donc en adaptation d'impédence, on a donc Zcâble = Rvariable.
A l'aide d'une mesure à l'ohmètre, nous avons Rvariable = 50,5Ω

Transmission d'impultions dans un câble coaxial : réflexion et adaptation
Nous venons de caractériser les paramètres physiques du câble coaxial. Nous allons à présent étudier la transmitission d'impultions en fonction de différents types d'impédances de charge. On utilise les mêmes conditions d'exitaion de câble coaxial que précédemment.
L'extrémité du câble étant ouverte, nous relevons et cotons les signaux V1 (entrée du câble), V2 (point milieu) et V3 (sortie du câble) en amplitude et en temps, nous obtenons donc la figure 11 ci-dessous.

figure 11 : tableau de mesures en amplitude et en temps de V1, V2 et V3
Nous pouvons ensuite tracer le diagramme de réflexion en figure 12 ci-dessous.
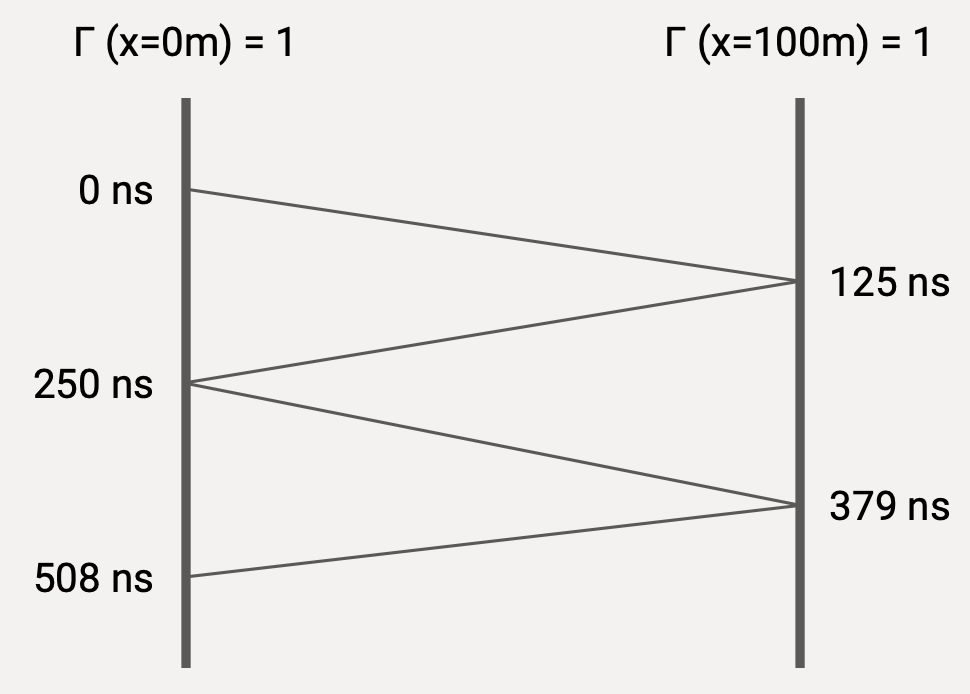
figure 12 : diagramme de réflexion d'un cabl coaxial en cirsuit ouvert

