Introduction :
Un condensateur possède son propre modèle électrique équivalent qui intègre les effets capacitifs mais également parasites comme les pertes diélectriques du matériau isolant et les effets de connectique selfique prépondérant à haute fréquences. Ces éléments peuvent être déterminées à partir du tracé de la variation du module de l'impédance (ou de l'admittance) en fonction de la fréquence. Ces éléments parasites influent fortement la fonction "découplage" d'un condensateur notamment car ils contribuent à diminuer sa fréquence de résonance.
Description des équipements et du logiciel utilisés
La mesure du comportement de composants passifs est possible par l'utilisation d'un équipement spécifique et relativement coûteux : l'analyseur de réseaux ou VNA.
Il permet de mesurer les paramètres S d'un quadripôle. L'analyseur de réseaux permet de mesurer simultanément la réflexion et la transmission générées par le dispositif à caractériser.
Pour ce TP, nous utiliserons un VNA de type ZVL de Rohde & Schwarz comme le montre la figure 1 ci-dessous.

figure 1 : analyseur de réseaux utilisé lors de ce TP
Le comporteùent fréquentiel des composants passifs consiste en la mesure de module de l'impédance en fonction de la fréquence. Pour cela, l'analyseur de réseaux mesure les paramètres S puis déduit l'impédance Z (module et phase) par le biais de la même transformation mathématique que celle utilisée dans l'abaque de Smith : Z = Z0 * ((1+Γ)/(1-Γ)).
Pour effectuer des mesures précises, l'appareil doit au préalable être calibré, sinon on ne mesure pas les vrais paramètres S du quadripôle mais ceux du quadripôle en cascade avec les câbles de mesure et la connectique associée. Pour calibrer l'appareil, on doit utiliser des charges spécifiques comme indiqué en figure 2. Elles sont au nombre de trois :
circuit ouvert
court-circuit
charge de 50Ω
La procédure de calibration est similaire à celle que l'on utilise pour la mesure d'une résistance avec un ohmmètre par exemple. En effet, il faut soustraire la résistancedes fils de mesure pour obtenir la vraie valeur de al résistance sous test.
Après calibration, tout se passe comme si la source était directement appliquée à l'entrée du quadripôle.
L'analyseur permet des mesures dans une bande de fréquence donnée et la calibration doit impérativement se faire dans la même bande de fréquence après avoir fixé le format d'affichage des données.
Etude de la phase de calibration et mesure de l'impédance d'un condensateur discret
Configurer le domaine d'analyse de l'appareil
Avant toute configuration, il est sain de remettre à plat toute configuration antérieure : [PRESET] → OK
Nous fixons ensuite les paramètres suivants :
Fréquence de départ : [START] = 30kHz
Fréquence d'arrêt : [STOP] = 900MHz
Nombre de points : [SWEEP SETUP] → points = 1001
Facteur de moyennage [AVG] → AVG factor = 10
Balayage fréquenciel [SWEEP SETUP] → sweep type = log sweep
Configurer l'affichage de la mesure
Afin d'afficher correctement et exploiter au mieux les résultats, nous fixons les parapètres suivants :
Mesure du coefficient de réflexion : [MEAS] → Network analysis menu = S11
Affichage du coefficient de réflexion sur l'abaque de Smith [FORMAT] → Smith = R+jX
Calibrage
Nous pouvons ensuite calibrer l'appareil dans la gamme de fréquences que nous avons fixé plus tôt à l'aide d'un kit de calibration comme le montre la figure 2 ci-dessous, afin de faire la calibration la plus rpécise possible, nous cherchons à minimiser le plus possible les courbures eventuelles du câble coaxial.

figure 2 : kit de calibration utilisée pour calibrer le VNA
Nous pouvons ensuite lancer la procédure de calibration du VNA.
Tout d'abord, nous devons charger les imperfections des standards de référence : [CAL] → Cal kit = SMD 50 ohm GEII
Mesure des standards de références : [CAL] → Calibrate → 1 port Cal
Brancher le circuit ouvert puis, nous lançons la mesure en appuyant sur OPEN
Brancher le court-circuit puis, nous lançons la mesure en appuyant sur SHORT
Brancher la charge Z0 = 50Ω puis, nous lançons la mesure en appuyant sur LOAD
Une fois la calibration terminée, nous pouvons compérer les résultats obtenu en figure 3 aux résultats attendu en figure 4 ci-dessous, nous pouvons lancer le calcul des erreurs systématiques entre l'appareil et le bout du câble en appuyant sur DONE.
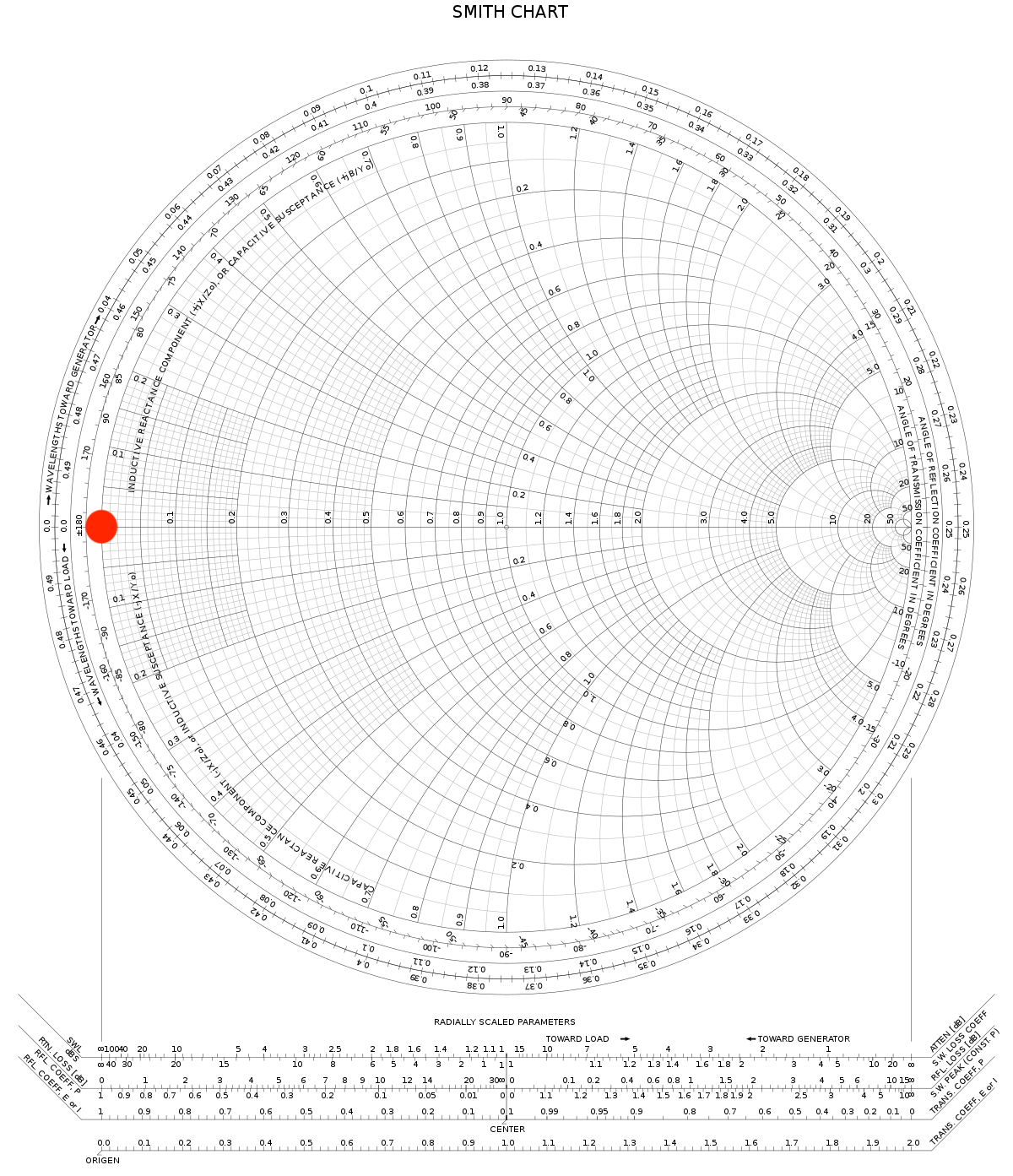
résultat attendu pour Z = 0 + 0j
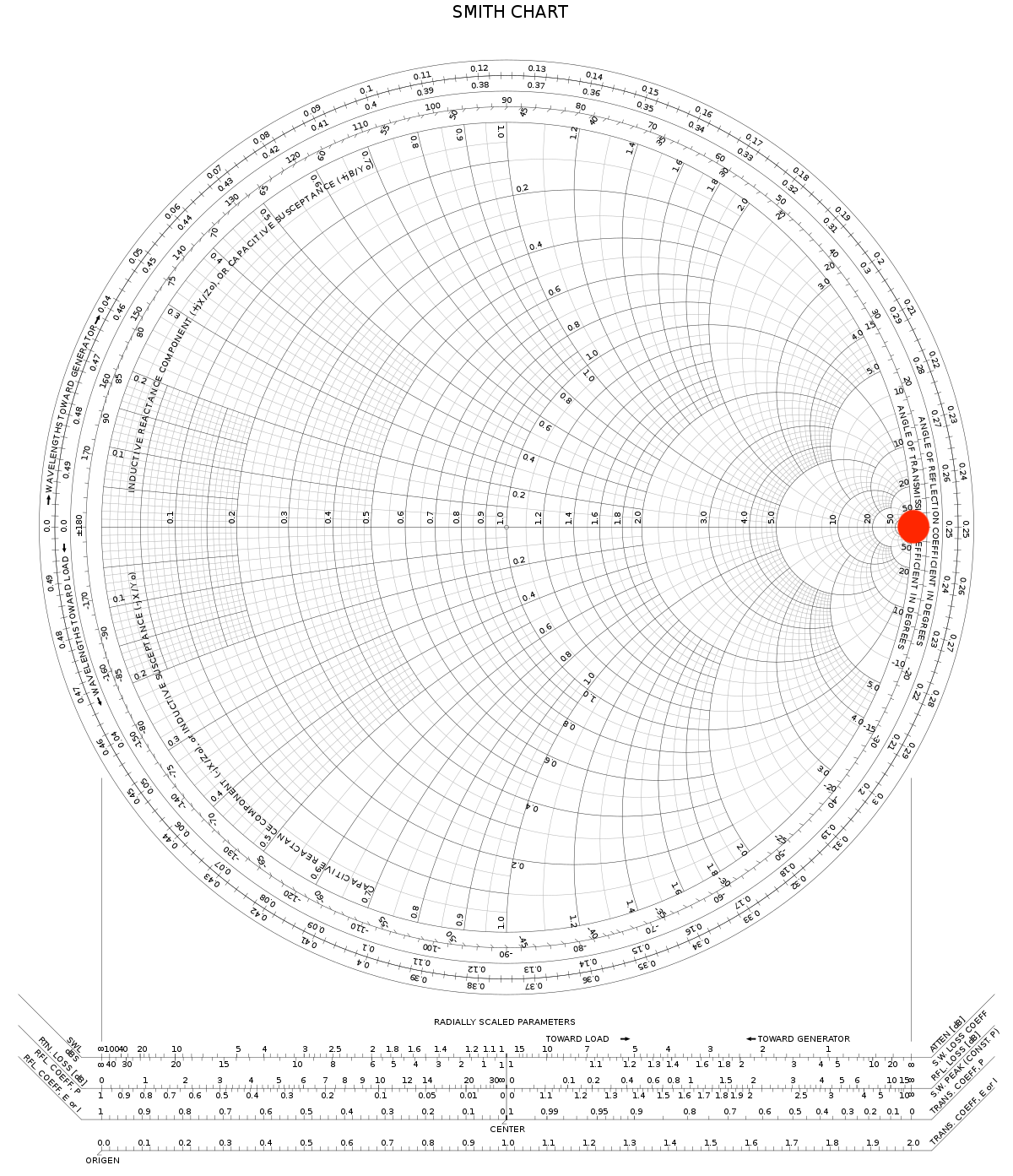
résultat attendu pour Z = +∞ + 0j
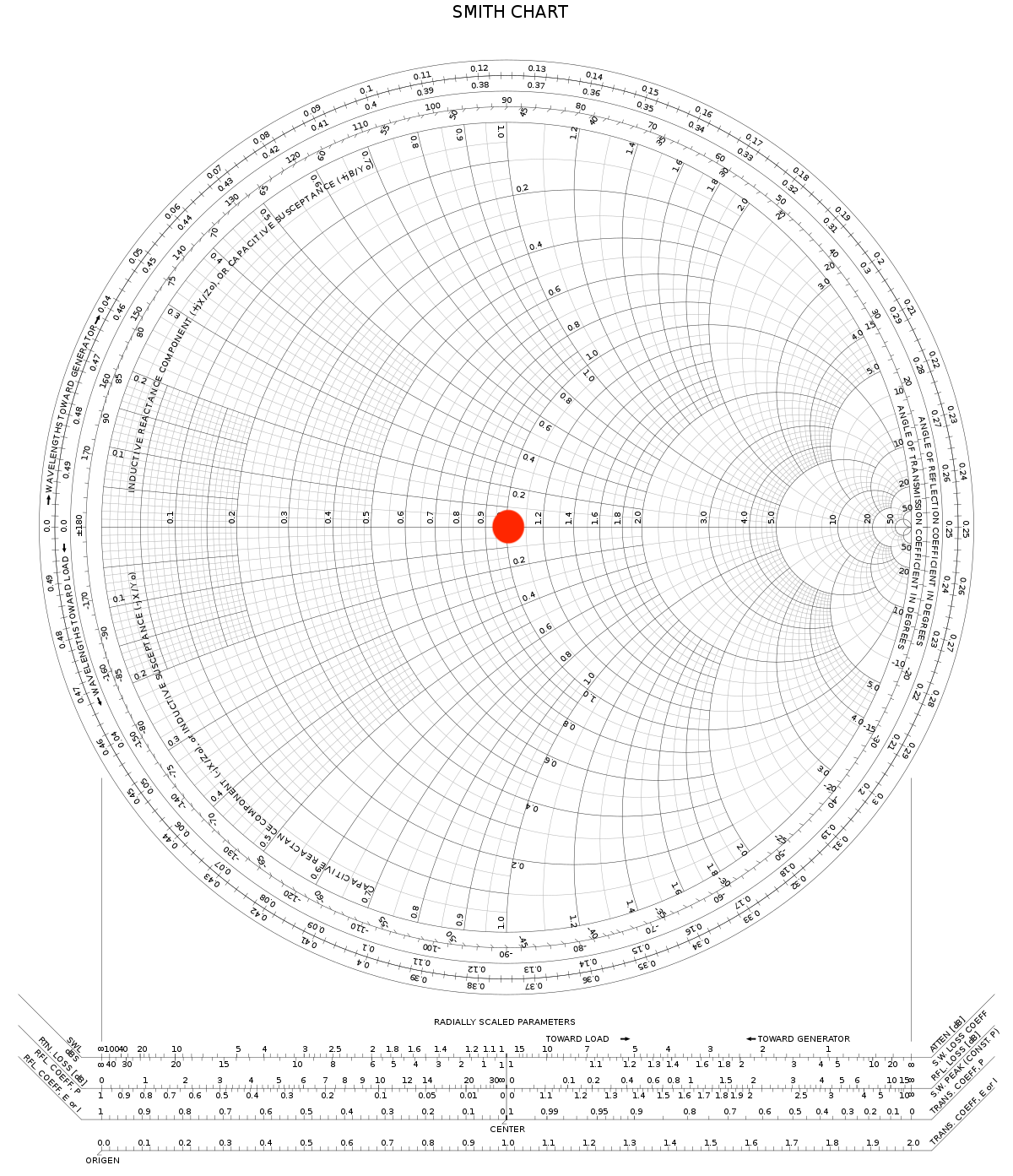
résultat attendu pour Z = 50Ω + 0j
figure 4 : résultats attendu pour la LOAD, l'OPEN et le SHORT
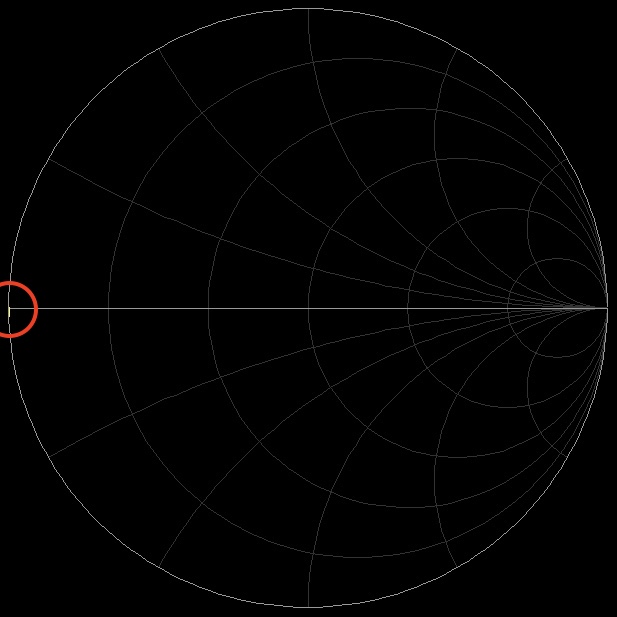
résultat obtenu : Z = -9e-3 + j13,5e-3
résultat obtenu : Z = -50e3 + j22e-3

résultat obtenu : Z = 50 + j13,5e-3
figure 3 : résultats obtenu pour la LOAD, l'OPEN et le SHORT
Une fois la calibration faite, nous devons étendre le plan de référence afin de mesurer non pas au niveau du connecteur mais au niveau du composant à mesurer.
Pour cela nous alons dans [CAL] → Port extension → 1 port Cal → ON, puis nous réglons le temps à 107ps
Ensuite, nous configurons le VNA pour ne plus afficher le coefficient de reflexion, mais l'impédance :
afficher le module de l'impedance : [MEAS] → impedance analysis menu → ⎟Z⎟
configurer l'affichage vertical en log : [SCALE] → Y axis → log
adapter l'affichage pour tout voir : [SCALE] → autoscale
Ajout d'un marqueur : [MARKER] → Marker 1
Caractérisation d'un condensateur traversant
Afin de carractériser le condensateur, nous branchons le condensateur au VNA à l'aide du câble coaxial comme le montre la figure 5 ci-dessous.


figure 5 : plaque de test avec le condensateur à caractériser (en rouge) et câblage au VNA
Nous pouvons donc relever l'ensemble des points mesurée par le VNA dans un fichier en .csv que nous pouvons exploiter dans Qucs. La simulation sous qucs nous permets de reproduire les réusltats affichés par le VNA et de carractériser les ocmposants mesuré, dans ce cas il s'agit d'un condensateur THD dont le scéma équivalent est représenté en figure 6 ci-desous.

figure 6 : schéma équivalent d'un condensateur réel
Afin de pouvoir carractériser ce condensateur, nous reproduisons sa réponse en fréquence sous qucs à l'aide du fichier csv généré par le VNA comme le montre la figure 7 ci-dessous.
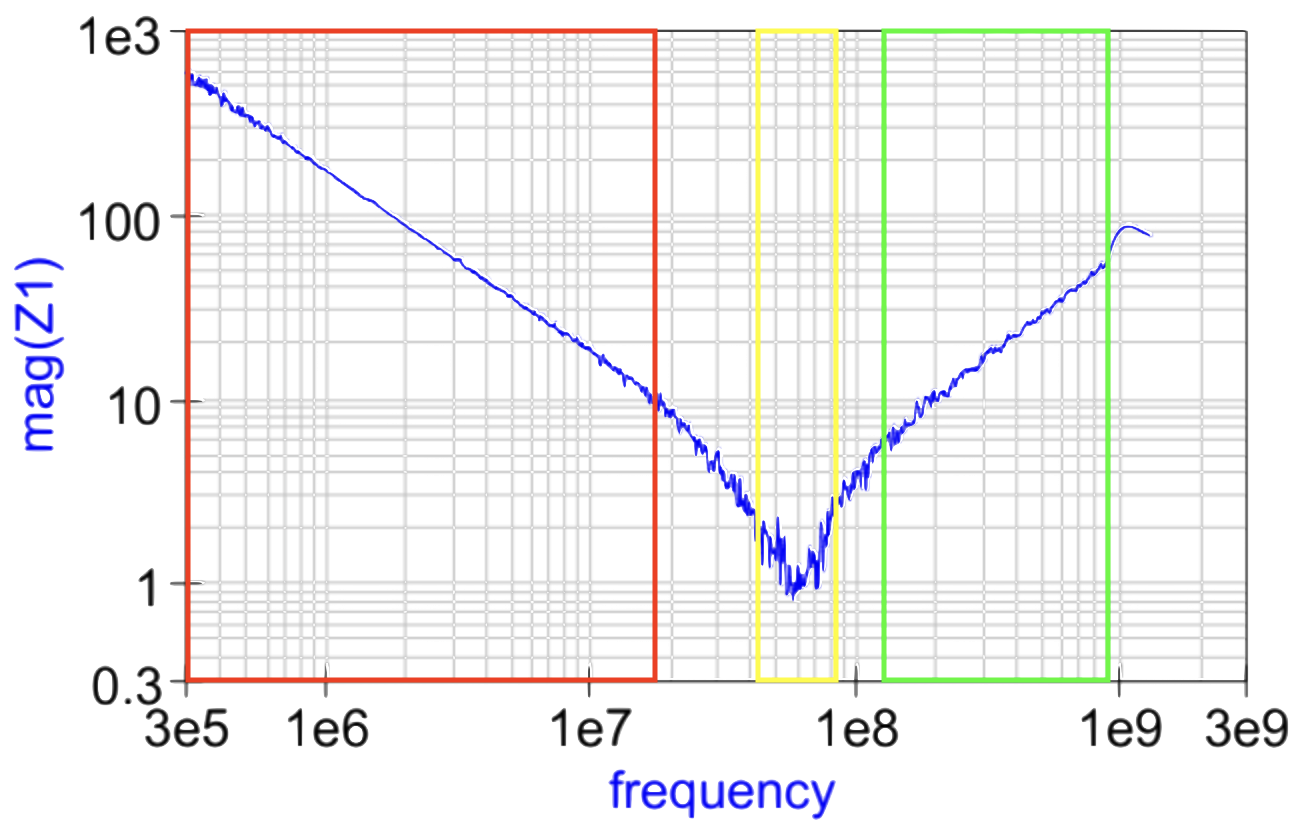
figure 7 : réponse en fréquence d'un condensateur réel
En fonction de la fréquence, un condensateur peut avoir des comportements très différents, nous pouvons voir sur la réponse en fréquence ci-dessus qu'entre 300kHz et 20MHz (zone en rouge), le condensateur à un comportement capacitif, entre 100MHz et 1GHz (zone en vert), le condensateur adopte en comportement inductif et aux alentours de 60MHz se trouve sa fréquence de résonnance.
A l'aide de qucs, nous plaçons un point dans chacune de ses zones stratégiques comme le montre la figure 8 ci-dessous, afin de déterminer son schéma équivalent.

figure 8 : points de mesure pour le condensateur THD
Comme nous le montre la figure 9 ci-dessous, à l'aide de ses 3 points de mesures, nous pouvons donc calculer l'inductance et la résistance parasite ainsi que la capacité du condensateur THD.

figure 9 : caractérisation du condensateur
Nous pouvons voir que la simulation qucs en figure 9 ci-dessus se compose de 5 parties distinctes, l'affichage des résultats obtenu à l'aide du VNA ou on peut notament y trouver la réponse du gain et de la phase en fonction de la fréquence, ses graphiques nous servirons à carractériser le composant dans les parties suivantes, nous trouvons également l'abaque de smith du composant.
La seconde partie est le carractérisation de la partie capacitive du composant ainsi que la réponse en fréquence théorique comme le montre la figure 10 ci-dessous, le calcul de la capaciée se fait à l'aide d'un point judicieusement placé comme expliqué précédament, et nous appliquons ensuite la formule de l'impédance d'un condensateur : C = 1/(R*ω) = 1/(32,5*2*pi*5,42e6) = 904pf.
La troisième partie consiste à mesurer la résistance parasite ainsi que la fréquence de résonance du composant au point le plus bas de la réponse en fréquence comme le montre la figure 10 ci-dessous, nous avons donc R = 0,823Ω et fr = 58,4MHz.
La quatrième partie consiste à calculer l'inductance parasite du condensateur se fait à l'aide d'un point judicieusement placé comme expliqué précédament, et de la formule de l'impédance d'une bobine : L = R/ω = 11/2*pi*212e6 = 8,26nH.
La cinquième partie est la conclusion de cette simulation et affiche le schéma équivalent de ce composant avec les valeurs de composants calculées précédament comme le montre la figure 11 ci-dessous.

figure 10 : Comparaison de la réponse en fréquence théorique (Z2 condensateur, Z3 inductance) à celle mesurée (en bleu)

figure 11 : schéma équivalent du condensateur étudié
Caractérisation d'un condensateur CMS
Afin de carractériser le condensateur nous appliquons la même démarche que pour le condensateur traversant mais cette fois-ci, nous branchons le condensateur CMS au VNA à l'aide du câble coaxial comme le montre la figure 12 ci-dessous.
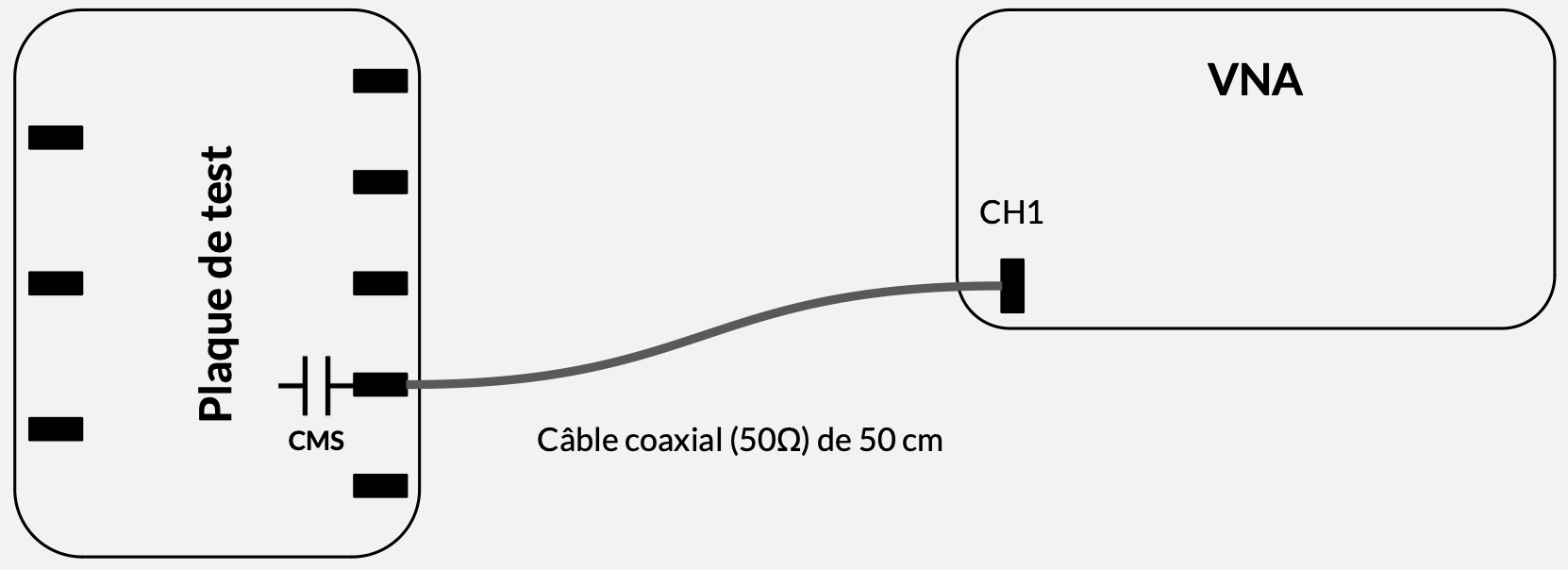
figure 12 : câblage au VNA du condensateur à caractériser
Une fois le nouveau fichier csv récupéré du VNA, nous pouvons refaire les démarches mais avec les 3 nouveaux points qui correspondent au condensateur CMS et nous permet donc d'obtenir une nouvelle simulation comme le montre la figure 13 ci-dessous.

figure 13 : caractérisation du condensateur CMS
Nous pouvons voir que la simulation qucs en figure 13 ci-dessus se compose de 5 parties distinctes, l'affichage des résultats obtenu à l'aide du VNA ou on peut notament y trouver la réponse du gain et de la phase en fonction de la fréquence, ses graphiques nous servirons à carractériser le composant dans les parties suivantes, nous trouvons également l'abaque de smith du composant.
La seconde partie est le carractérisation de la partie capacitive du composant ainsi que la réponse en fréquence théorique comme le montre la figure 14 ci-dessous, le calcul de la capaciée se fait à l'aide d'un point judicieusement placé comme expliqué précédament, et nous appliquons ensuite la formule de l'impédance d'un condensateur : C = 1/(R*ω) = 1/(69,4*2*pi*215e6) = 10,7pf.
La troisième partie consiste à mesurer la résistance parasite ainsi que la fréquence de résonance du composant au point le plus bas de la réponse en fréquence comme le montre la figure 14 ci-dessous, nous avons donc R = 9,11Ω et fr = 892MHz.
La quatrième partie consiste à calculer l'inductance parasite du condensateur se fait à l'aide d'un point judicieusement placé comme expliqué précédament, et de la formule de l'impédance d'une bobine : L = R/ω = 70,7/2*pi*1,3e9 = 8,66nH.
La cinquième partie est la conclusion de cette simulation et affiche le schéma équivalent de ce composant avec les valeurs de composants calculées précédament comme le montre la figure 15 ci-dessous.
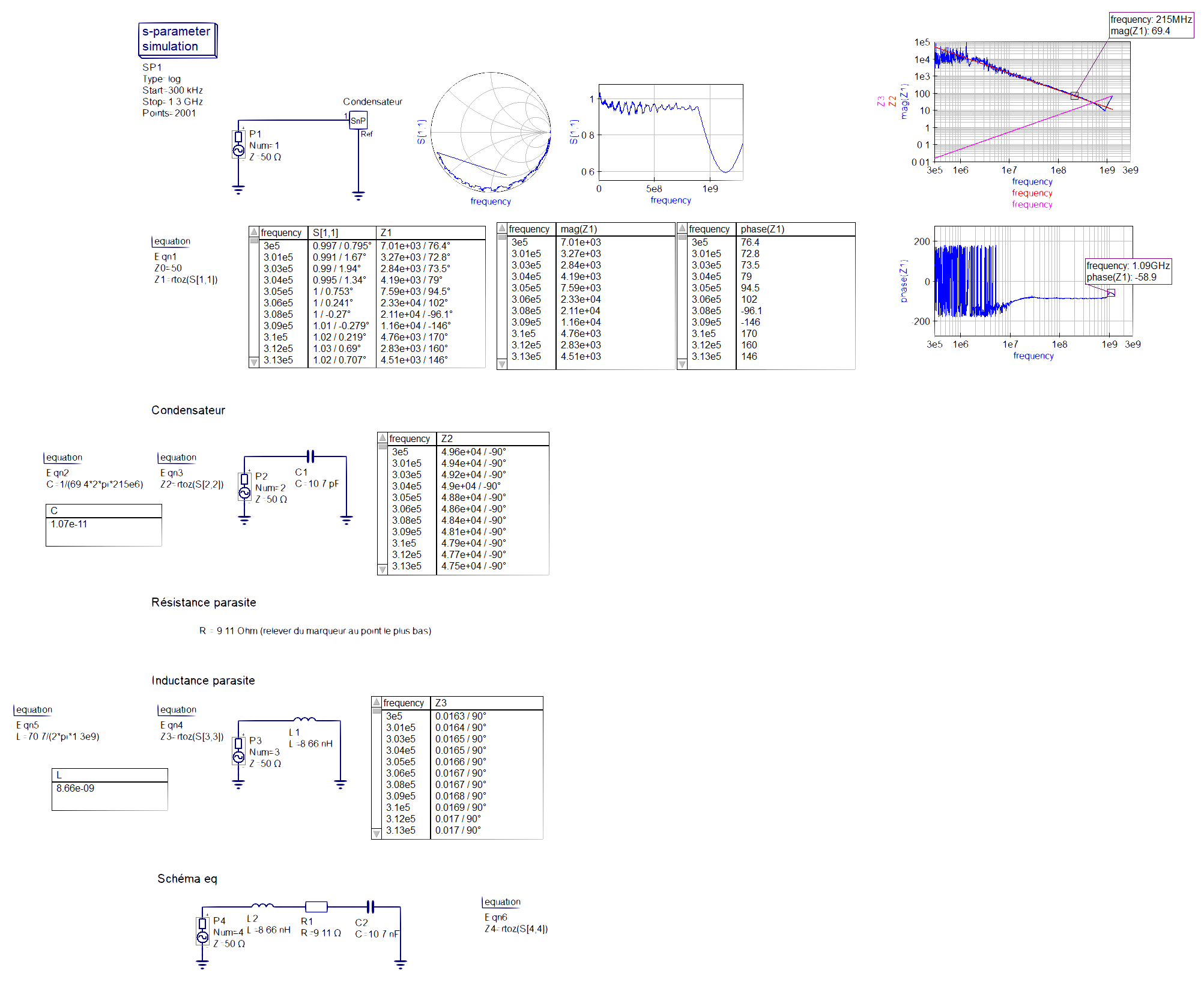
figure 14 : Comparaison de la réponse en fréquence théorique (Z2 condensateur, Z3 inductance) à celle mesurée (en bleu)
A ce moment là, nous pouvons voir que la valeur calculée de l'inductance est fausse car la droite Z3 qui correspond à la réponse en fréquence théorique du condensateur en régime inductif ne correspond pas aux mesures faites sur le VNA. Etant donné que cette méthode de calcul à déja été utilisée pour carractériser le condensateur traversant, de plus, le tracé de la phase en fonction de la fréquence ne ressemble pas au résultat auquel on s'attend, ni à la phase mesurée pour le condensateur traversant.
Nous avons donc conclu qu'afin de résoudre ce problème nous recommandons de refaire la mesure du condensateur à l'aide du VNA afin d'en extraire un nouveau fichier csv valide.
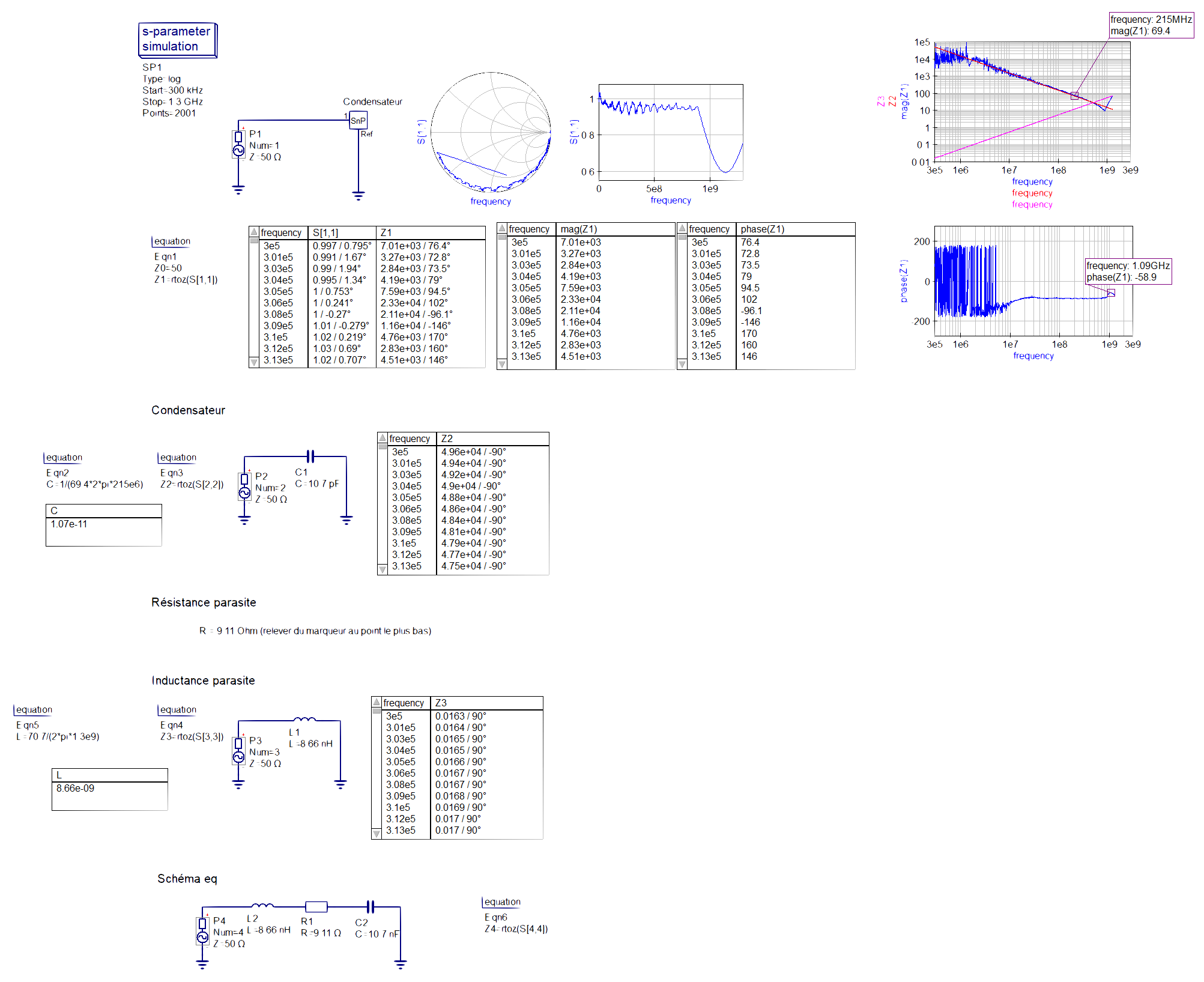
figure 15 : schéma équivalent du condensateur CMS étudié
Caractérisation d'une inductance
Afin de caractériser l'inductance nous appliquons la même démarche que pour les condensateurs mais cette fois-ci, nous branchons le condensateur CMS au VNA à l'aide du câble coaxial comme le montre la figure 16 ci-dessous.

figure 16 : câblage au VNA du condensateur à caractériser
Une fois le nouveau fichier csv récupéré du VNA, nous pouvons refaire les démarches mais avec les 3 nouveaux points qui correspondent au condensateur CMS et nous permet donc d'obtenir une nouvelle simulation comme le montre la figure 17 ci-dessous.

figure 17 : caractérisation d'une inductance
Nous pouvons voir que la simulation qucs en figure 17 ci-dessus se compose de 5 parties distinctes, l'affichage des résultats obtenu à l'aide du VNA ou on peut notament y trouver la réponse du gain et de la phase en fonction de la fréquence, ses graphiques nous servirons à carractériser le composant dans les parties suivantes, nous trouvons également l'abaque de smith du composant.
La seconde partie est le carractérisation de la partie capacitive du composant ainsi que la réponse en fréquence théorique comme le montre la figure 18 ci-dessous, le calcul de la capaciée se fait à l'aide d'un point judicieusement placé comme expliqué précédament, et nous appliquons ensuite la formule de l'impédance d'un condensateur : C = 1/(R*ω) = 1/(439*2*pi*480e6) = 0.92pf.
La troisième partie consiste à mesurer la résistance parasite ainsi que la fréquence de résonance du composant au point le plus haut de la réponse en fréquence comme le montre la figure 18 ci-dessous, nous avons donc R = 39.3 kΩ et fr = 210MHz.
La quatrième partie consiste à calculer l'inductance parasite du condensateur se fait à l'aide d'un point judicieusement placé comme expliqué précédament, et de la formule de l'impédance d'une bobine : L = R/ω = 80.1/2*pi*22e6 = 579nH.
La cinquième partie est la conclusion de cette simulation et affiche le schéma équivalent de ce composant avec les valeurs de composants calculées précédament comme le montre la figure 19 ci-dessous.
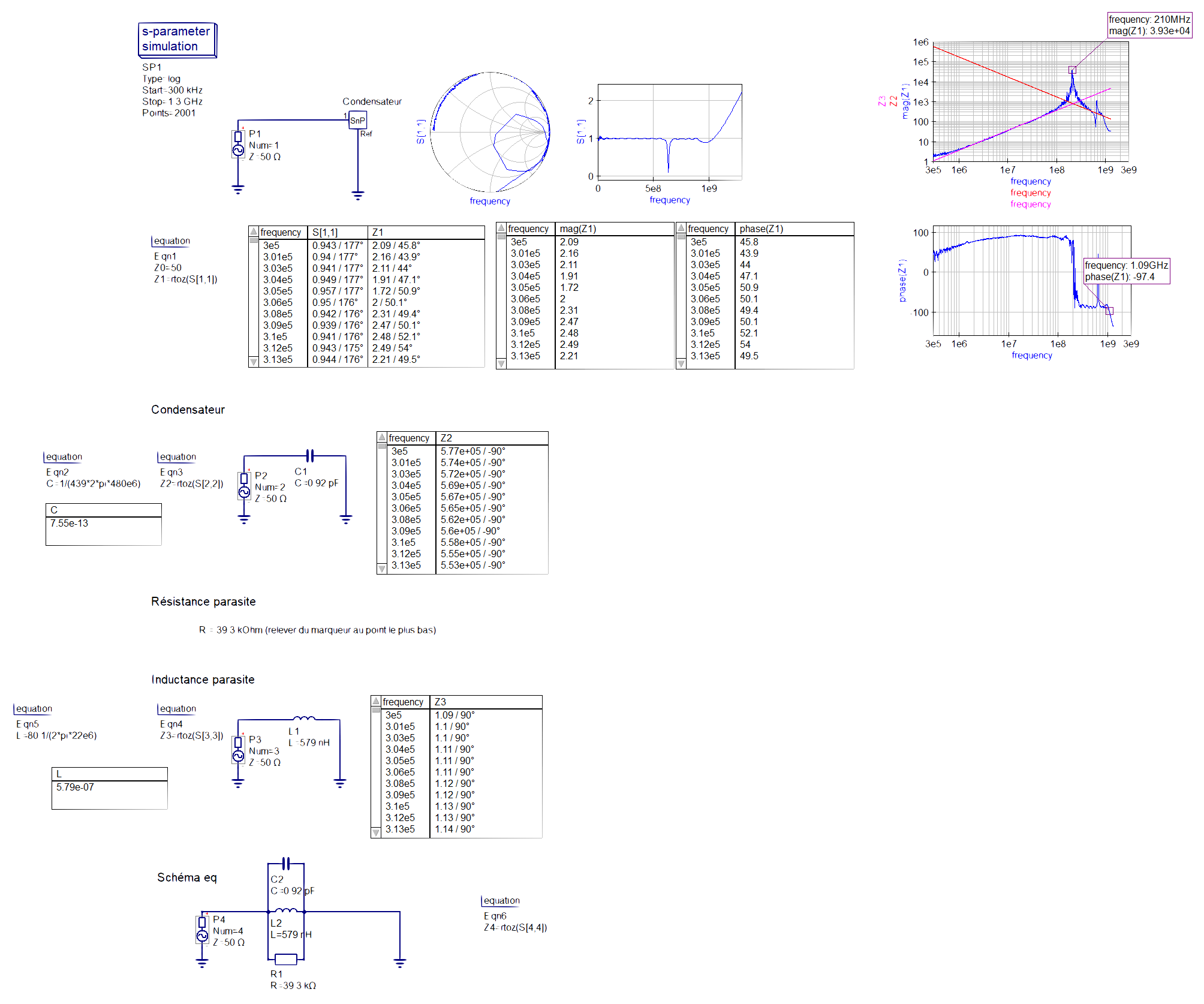
figure 18 : Comparaison de la réponse en fréquence théorique (Z2 condensateur, Z3 inductance) à celle mesurée (en bleu)
A ce moment là, nous pouvons voir que la valeur calculée de l'inductance est fausse car la droite Z3 qui correspond à la réponse en fréquence théorique du condensateur en régime inductif ne correspond pas aux mesures faites sur le VNA. Etant donné que cette méthode de calcul à déja été utilisée pour carractériser le condensateur traversant, de plus, le tracé de la phase en fonction de la fréquence ne ressemble pas au résultat auquel on s'attend, ni à la phase mesurée pour le condensateur traversant.
Nous avons donc conclu qu'afin de résoudre ce problème nous recommandons de refaire la mesure du condensateur à l'aide du VNA afin d'en extraire un nouveau fichier csv valide.

figure 19 : schéma équivalent de l'inductance étudié
